 |
| Gradien adalah kemiringan suatu garis. |
sedangkan Garis Lurus adalah garis yang menghubungkan dua titik. Persamaan garis lurus menunjukkan perbandingan komponen y dan komponen x yang dilalui titik yang dimaksud.
Menentukan gradien garis berdasarkan gambar
komponen perpindahan vertikal (y)
komponen perpindahan horisontal (x)
Komponen y ke atas bernilai positif, sedangkan jika ke arah bawah bernilai negatif.
Komponen x ke kanan bernilai positif, sedangkan jika ke kiri bernilai negatif.
Perhatikan gambar berikut !
 |
| Gambar 1 |
Gradien garis m= ke atas 2 satuan = 2 = 1
ke bawah 4 satuan 4 2
Untuk menghitung gradien garis yang melalui dua titik (x1,y1) dan (x2,y2) digunakan rumus berikut:
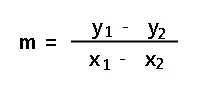 |
| Rumus |
Perhatikan gambar berikut !
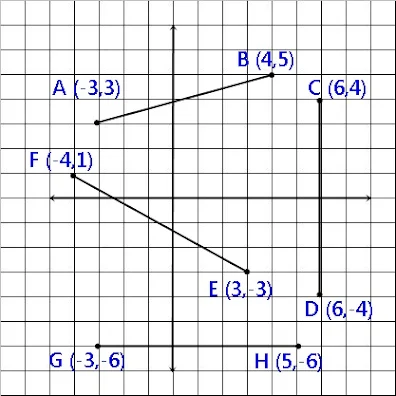 |
| Gambar 2 |
mAB= 3 - 5 = -2 = 2
-3 - 4 -7 7
mCD= 4 - (-4) = 8 =∽ , kesimpulan : garis yang sejajar sumbu y memiliki gradien=∽
6 - 6 0
mEF= -3 - 1 = -4
3 - (-4) 7mGH= -6 - (-6) = 0 = 0 , kesimpulan : garis yang sejajar sumbu x memiliki gradien=0
-3 - 5 -8
Menentukan gradien dari persamaan garis
Bentuk persamaan y=mx + c , memiliki gradien=m
Bentuk persamaan ax + by=c, memiliki gradien=-a/b
Contoh :
1. Garis y=½ x, gradiennya=½
2. Garis y=-3x + 5 , gradiennya=-3
3. Garis 5x - 4y=20, gradiennya=-5/-4=5/4
Garis yang saling sejajar dan garis yang saling tegak lurus
Perhatikan gambar berikut !
 |
| Gambar 3 |
Garis k melalui titik (1,0) dan (5,3) sehingga gradiennya 3/4
Garis l melalui titik (4,0) dan (0,-3) sehingga gradiennya 3/4
Garis m melalui titik (4,-4) dan (1,0) sehingga gradiennya -4/3
Dari gambar di atas terlihat bahwa garis k dan garis l saling sejajar dan memiliki gradien sama. Maka kesimpulannya adalah dua garis yang saling sejajar memiliki hubungan m1=m2
Garis m terlihat kedudukannya tegak lurus terhadap garis k maupun garis l.
Gradien garis k=3/4, sedangkan gradien garis m= -4/3.
3/4 x -4/3=-1
Maka dua garis yang saling tegak lurus memiliki hubungan m1 x m2=-1, atau m2=-1/m1.
Menentukan titik potong sumbu x dan sumbu y suatu garis
Garis y=mx
memiliki gradien m dan melalui titik O (0,0)
Garis y=mx + c
memiliki gradien m dan melalui titik (0,c)
Garis ax + by=c
memiliki gradien -a/b
titik potong sumbu x yaitu jika y=0, maka titik potongnya (-c/a , 0)
titik potong sumbu y yaitu jika x=0, maka titik potongnya (0, -c/b)
2. Persamaan y=⅔ x - 5 melalui titik (0, -5)
Jawaban : b
3. Perhatikan gambar !
ke atas 2 satuan = 2
ke kiri 5 satuan -5
maka gradien garis h=-2/5
Jawaban : b
4. Melalui titik O (0,0) dan P (12, -9)
= 0 - (-9) = 9 =- 3
0 - 12 -12 4
Jawaban : b
5. A (-4,7) dan B (2, -2)
m= 7 - (-2) = 9 = -3
-4 - 2 -6 2
Jawaban=a
6. Persamaan 2x + 6y=15
a=2, b=6
m=-a/b=-2/6=-1/3
Jawaban=b
7. A (1,4) dan B (3,p) sejajar dengan garis y=3x -2
m1=m2
4 - p =3
1 - 3
4 - p =3
-2
4 - p=3 x -2
4 - p=-6
- p=- 6 - 4
- p=-10
p=10
jawaban : a
8. Gradien dari persamaan
memiliki gradien m dan melalui titik O (0,0)
Garis y=mx + c
memiliki gradien m dan melalui titik (0,c)
Garis ax + by=c
memiliki gradien -a/b
titik potong sumbu x yaitu jika y=0, maka titik potongnya (-c/a , 0)
titik potong sumbu y yaitu jika x=0, maka titik potongnya (0, -c/b)
Menentukan persamaan garis
Jika diketahui garis bergradien m dan melalui satu titik (x1,y1)
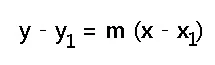 |
| rumus 2 |
Jika diketahui garis melalui dua titik (x1,y1) dan (x2,y2)
 |
| rumus 3 |
Contoh soal :
1. Gambar yang menunjukkan garis dengan persamaan y=1½ x adalah.....
 |
| Gambar 4 |
2. Titik berikut yang terletak pada garis y=⅔ x - 5 adalah....
a. A (2 , 3) c. C (- 5, 0)
b. B (0 , -5) d. D (0 , 5)
3. Gradien garis h pada gambar di bawah adalah....
 |
| Gambar 5 |
a. 2/5 b. -2/5 c. 5/2 d. -5/2
4. Gradien garis yang melalui titik O dan titik P (12, -9) adalah...
a. -4/3 b. -3/4 c. 3/4 d. 4/3
5. Gradien garis yang melalui titik A (-4,7) dan B (2, -2) adalah....
a. -3/2 b. -2/3 c. 2/3 d. 3/2
6. Gradien dari garis dengan persamaan 2x + 6y=15 adalah....
a. -3 b. -1/3 c. 1/3 d. 3
7. Garis AB yang melalui titik A (1,4) dan B (3,p) sejajar dengan garis yang persamaannya y=3x -2. Maka nilai p yang memenuhi adalah....
a. 10 b. 8 c. 2 d. -2
8. Perhatikan persamaan-persamaan garis berikut !
I. x + 2y=5
II. 2x + y=9
III. 2x - y=3
IV. y=-2x + 8
Dua garis yang saling tegak lurus adalah....
a. I dan II b. II dan III c. I dan III d. II dan IV
9. Persamaan garis yang bergradien -4 dan melalui titik (0,3) adalah....
a. y=4x + 3 c. y=3x + 4
b. y=-4x + 3 d. y=3x - 4
10. Jika suatu garis memilki persamaan 3x -5y -10=0, maka
I. bergradien 3/5
II. melalui titik (0, -2)
III.sejajar dengan garis y=5/3 x -5
IV. tegak lurus dengan garis y=-5/3 x + 4
Pernyataan yang benar adalah....
a. I dan II b. I dan III c. II dan III d. II dan IV
11. Persamaan garis yang melalui titik (-2,-2) dan (4,1) adalah....
a. 2x + 3y=6 c. 2x + y=2
b. x + y=8 d. x - 2y=2
12. Persamaan garis yang melalui titik (2, -7) dan tegak lurus garis 4x - 3y + 8=0 adalah...
a. 3x - 4y=34 c. 3x + 4y=-22
b. 4x + 3y=-13 d. 4x - 3y=21
13. Persamaan garis yang melalui titik (-2,3) dan sejajar garis 2x + 4y=5 adalah....
a. 2x - y + 4=0 c. x - 2y=-4
b. 2x + y=4 d. x + 2y=4
14. Persamaan garis yang melalui titik (4, -6) dan sejajar dengan garis yang melalui titik (3, -4) dan (6, 2) adalah....
a. y=½ x - 8 c. y=2x - 14
b. y= ½ x + 4 d. y=2x - 2
15. Tiga titik P (-1,3a), Q (3 , -2) dan R (1 , a) berada dalam satu garis lurus. Tentukan nilai a yang memenuhi !
a. -2 b. - 1 c. 1 d. 2
1. Persamaan y=1½ x, melalui titik (0,0) dan bergradien 1½=3/2
komponen y = 3
komponen x 2
Jawaban : c11. Persamaan garis yang melalui titik (-2,-2) dan (4,1) adalah....
a. 2x + 3y=6 c. 2x + y=2
b. x + y=8 d. x - 2y=2
12. Persamaan garis yang melalui titik (2, -7) dan tegak lurus garis 4x - 3y + 8=0 adalah...
a. 3x - 4y=34 c. 3x + 4y=-22
b. 4x + 3y=-13 d. 4x - 3y=21
13. Persamaan garis yang melalui titik (-2,3) dan sejajar garis 2x + 4y=5 adalah....
a. 2x - y + 4=0 c. x - 2y=-4
b. 2x + y=4 d. x + 2y=4
14. Persamaan garis yang melalui titik (4, -6) dan sejajar dengan garis yang melalui titik (3, -4) dan (6, 2) adalah....
a. y=½ x - 8 c. y=2x - 14
b. y= ½ x + 4 d. y=2x - 2
15. Tiga titik P (-1,3a), Q (3 , -2) dan R (1 , a) berada dalam satu garis lurus. Tentukan nilai a yang memenuhi !
a. -2 b. - 1 c. 1 d. 2
Pembahasan
1. Persamaan y=1½ x, melalui titik (0,0) dan bergradien 1½=3/2
komponen y = 3
komponen x 2
2. Persamaan y=⅔ x - 5 melalui titik (0, -5)
Jawaban : b
3. Perhatikan gambar !
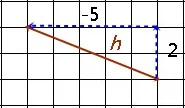 |
| Gambar 6 |
ke kiri 5 satuan -5
maka gradien garis h=-2/5
Jawaban : b
4. Melalui titik O (0,0) dan P (12, -9)
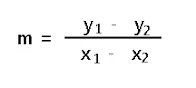 |
| rumus 4 |
= 0 - (-9) = 9 =- 3
0 - 12 -12 4
Jawaban : b
5. A (-4,7) dan B (2, -2)
m= 7 - (-2) = 9 = -3
-4 - 2 -6 2
Jawaban=a
6. Persamaan 2x + 6y=15
a=2, b=6
m=-a/b=-2/6=-1/3
Jawaban=b
7. A (1,4) dan B (3,p) sejajar dengan garis y=3x -2
m1=m2
4 - p =3
1 - 3
4 - p =3
-2
4 - p=3 x -2
4 - p=-6
- p=- 6 - 4
- p=-10
p=10
jawaban : a
8. Gradien dari persamaan
I. x + 2y=5 adalah -1/2
II. 2x + y=9 adalah -2
III. 2x - y=3 adalah -2/-1=2
IV. y=-2x + 8 adalah -2
Dua garis saling tegak lurus jika memenuhi m1 x m2=-1
Maka yang memenuhi adalah garis I dan III
Jawaban : c
9. Gradien -4 dan melalui titik (0,3)
Persamaan garisnya y=-4x + 3
Jawaban : b
10. Persamaan 3x -5y -10=0
I. gradien=-3/-5=3/5
II. jika x=0, maka
3(0) -5y - 10=0
0 - 5y=10
- 5y=10
y=10/-5=-2
melalui titik (0, -2)
III. m1 ≠ m2, maka tdak sejajar
IV. m1=3/5, m2=-5/3
m1 x m2=-1, maka tegak lurus
Jawaban : d
11. Melalui titik (-2,-2) dan (4,1)
 |
| rumus 5 |
y - (-2) = x - (-2)
1 - (-2) 4 - (-2)
y + 2 = x + 2 , (kali silang)
3 6
6y + 12 = 3x + 6
-3x + 6y =6 - 12
-3x + 6y =-6, (dibagi -3)
x - 2y =2
Jawaban : d
12. Melalui titik (2, -7) dan tegak lurus garis 4x - 3y + 8=0
m1=-4/-3=4/3
m2=-1/m1=-3/4
y - y1 =m (x - x1)
y - (-7)=-3/4 (x - 2)
y + 7 =-3/4 x + 3/2, (dikali 4)
4y + 28=-3x + 6
3x + 4y=6 - 28
3x + 4y=-22
Jawaban : c
13. Melalui titik (-2,3) dan sejajar garis 2x + 4y=5
m1=-2/4=-1/2
sejajar maka m1=m2
y - y1 =m (x - x1)
y - 3 =-1/2 (x -(-2))
y - 3 =-1/2 x -1, (dikali 2)
2y - 6=-x -2
x + 2y=-2 + 6
x + 2y=4
Jawaban : d
14. Melalui titik (4, -6) dan sejajar dengan garis yang melalui titik (3, -4) dan (6, 2)
m= -4 - 2 = -6 =2
3 - 6 -3
y - y1 =m (x - x1)
y - (-6)=2 (x - 4)
y + 6 =2x - 8
y =2x - 8 - 6
y =2x - 14
Jawaban : c
15. Titik P (-1,3a), Q (3 , -2) dan R (1 , a) dalam satu garis lurus
Untuk menyelesaikan soal seperti ini pergunakan rumus :
 |
| rumus 6 |
3a - (-2) = -2 - a
-1 - 3 3 - 1
3a + 2 = -2 - a , (kali silang)
-4 2
6a + 4 = 8 + 4a
6a - 4a = 8 - 4
2a = 4
a =4/2 =2
Jawaban : d
Semoga bermanfaat
